Process Variation

System Model > Statistical Process Control (SPC) > Process Variation

To use SPC effectively, understand the concept of variation. When a product characteristic is measured repeatedly, each measurement is likely to differ from the last. This is because the process contains sources of variability.

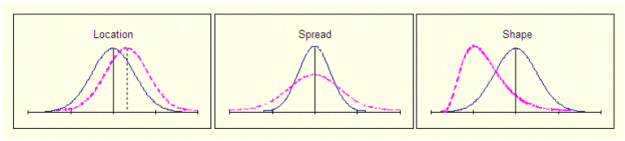
When the data is grouped into a frequency histogramA bar graph that shows frequency of occurrence versus value. Quite often the data is fitted to a distribution such as a normal distribution. ., it will tend to form a pattern. The pattern is referred to as a probability distribution and is characterized in three ways:

Note: Most SPC techniques assume that the collected data has a normal distributionAlso known as a `bell' curve, the normal distribution is the best known and widely applicable distribution. The distribution is symmetrical and popularly represents the laws of chance. 68.27% of the area lies between -1 sigma and +1 sigma, 95.45% between -2 sigma and+2 sigma, and 99.73% between -3 sigma and +3 sigma. The values of skewness and kurtosis are used to provide quantitative measures for normality. Assuming that at least 20 samples are used to construct a distribution, a good rule of thumb is to accept the data as a normal distribution when, -1.0 = skewness = 1.0 2 = kurtosis = 4..

Variation is generally categorized into one of two types:

Common: refers to variation that is predictable and repeatable over time. The distribution characteristics will be stable. Common variation could be due to consistent process inaccuracy or similar.

Statistics indicate that common variations account for about 85% of departures from process quality requirements. Usually these departures require solution at the management level.

Special: refers to variation that is not consistently present. When special variation occurs it will tend to change the distribution characteristics. The distribution is not stable over time.

Statistics indicate that special variations account for about 15% of departures from process quality requirements. Typically these departures require local action (equipment repair and so on) for solution.